Formula lui Euler are o mulţime de aplicaţii în matematică
şi în afara ei. În geometrie, o putem folosi ca să determinăm uşor poliedrele regulate, adică acelea cu toate feţele egale cu un acelaşi poligon regulat (în particular, egale între ele) şi cu proprietatea că în fiecare vârf se întâlnesc un acelaşi număr de feţe. Corpurile acestea solide erau cunoscute încă din Antichitate: se interesa de ele şcoala greacă, iar în Elemente sunt discutate în Cartea a XIII-a. Cum Platon le-a folosit mult în dialogul Timaios, au fost numite corpuri platonice. Există numai cinci, iar acest rezultat e unul dintre cele mai bune din geometria în spaţiu a şcolii greceşti. Cele cinci corpuri regulate sunt reprezentate în figura 4.20, TETRAEDRU
CUB
OCTAEDRU
DODECAEDRU
ICOSAEDRU
foc
pământ
aer
eter
apă
Figura 4.20
GEOMETRIA DIN ZILELE NOASTRE 193
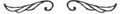
cu numele şi corespondenţa lor cu un element fundamental, aşa cum apar în Timaios.
Iată cum se poate demonstra existenţa a numai cinci poliedre regulate: să presupunem că feţele sunt triunghiuri regulate şi că în fiecare vârf se întâlnescx feţe. Dacă notăm cu/ numărul feţelor, rezultă că numărul laturilor trebuie să fie /= (3/2}/(pentru că fiecare latură stă pe două feţe), iar cel al vârfurilor (3/x}/.
Formula lui Euler devine:
2 = v - / + 1 = (i _ i + 1)/ = 6 - x f
X 2
2x
Deoarece în fiecare vârf trebuie să ajungă cel puţin trei feţe, soluţiile posibilesunt următoareletrei:x= 3,/=4;x=4,/= 8;x= S, f = 20, corespunzând tetraedrului, octaedrului şi icosaedrului.
La fel găsim alte două cazuri, cu feţele pătrate, respectiv pentagoane; în fine, procedând asemănător, se arată că nu e posibil să avem feţe regulate cu mai mult de cinci laturi.
Un poliedru convex poate fi „umflat", adică transformat în manieră continuă până devine o sferă; alături de demonstraţia pe care am indicat-o, observaţia aceasta ne spune că pavajele regulate ale sferei sunt exact cele cinci discutate mai înainte.
Am vorbit despre lipirea feţelor pentru a crea un poliedru, operaţie analoagă felului în care croitorul coase ( eventual după
ce a tăiat) bucăţi de stofă. Tăierea şi lipirea sunt operaţii bine definite şi în topologie, dar, prin definiţie, duc la schimbarea unor caracteristici topologice ale obiectului.
Să luăm două suprafeţe; o sumă conexă a lor constă în tăierea câte unui disc din fiecare şi lipirea celor două suprafeţe de-a lungul circumferinţelor celor
� �.·
două discuri. În figura 4.21 vedem
�· �
A
\
I B suma conexă dintre un covrig cu două găuri şi unul cu o singură
�
gaură, acesta din urmă numit tor.
�
Dacă suprafeţele sunt sufici
Figura 4.21
ent de regulate (de exemplu nu
194 FORMA LUCRURILOR










