Aşadar, dacă schimbăm doar un pic cuvintele, găsim aceleaşi concepte ca la Euclid.
Cu aceste patru proprietăţi, toţi sunt în stare să distingă o dreaptă fără nici o ambiguitate: e de ajuns să privim figura 2.1.
44
FORMA LUCRURILOR



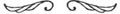
Prima imagine reprezintă o dreaptă (sim �tă
bolul săgeţii vrea să spună că dreapta se
prelungeşte la infinit). Dar celelalte trei
- nu: a doua are un capăt, e o semidreaptă.
În a treia, e evident că între unele dintre
punctele ei drumul cel mai scurt nu e cel
non drepte
de pe curbă. În a patra, dacă se scoate un
punct, nu rămân două bucăţi separate
(curba desenată are grosime).
Pe lângă cele patru caracteristici ale
dreptei, Euclid adaugă o a cincea, faimosul postulat al cincilea despre dreptele paralele. Pentru a-l formula, avem nevoie
de câteva definiţii pe care o să le luăm tot
Figura 2.1
din Elemente, dar nu chiar literal.
Definiţia 8. Unghiul plan e înclinarea reciprocă a două
drepte incidente într-un punct numit vârf.
Definiţia 9. Dacă cele două drepte care compun unghiul coincid, atunci unghiul se numeşte plat, iar măsura sa e n (în radiani; se poate alege şi măsura în grade, anume 180
de grade).
Unghiurile mai mici au măsuri proporţionale; de exemplu, avem următoarea definiţie:
Definiţia 1 O. Când o dreaptă
ridicată pe o alta formează
unghiuri adiacente egale între ele, fiecare unghi format se numeşte drept şi are măsura n/2 (90 de grade) (figura 2.2.).
Odată ce avem definiţia unghiului drept putem formula: Figura 2.2
CURBE
45

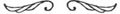
Figura 2.3
Postulatul 5. Şi că atunci când o dreaptă care taie alte două
drepte face cu ele în interior şi de aceeaşi parte unghiuri mai mici decât două unghiuri drepte, cele două drepte prelungite la infinit se întâlnesc de acea parte în care se află
unghiurile mai mici decât două unghiuri drepte.









