cercul există cu adevărat şi cum îl putem construi. O roată, profilul lunii pline şi atâtea alte forme se apropie de ideea de cerc, dar sunt cu adevărat cercuri? Cât despre construcţie, Euclid fentează problema postulând răspunsul.
Postulatul 3. Se trasează un cerc cu centru şi rază date.
În Şcoala din Atena, Rafael îl prezintă pe Euclid în timp ce desenează un cerc folosind un compas, adică un instrument articulat care păstrează fixă distanţa dintre puncte. De fapt, istoricii ştiinţei susţin că adevăratul compas e o invenţie arabă de după
Euclid; dar un mecanism mai rudimentar, poate cu un fir inextensibil sau cu o bară metalică, fixate la o extremitate şi dând posibilitatea celeilalte extremităţi să se mişte, un asemenea instrument sigur le era cunoscut grecilor.
Se zice că Giotto şi-ar fi uimit maestrul, pe Cimabue, desenând cercuri perfecte cu mâna goală; găsim o sugestie despre cum ar fi putut proceda într-un filmuleţ amuzant de pe You
Tube: https:/ / www.youtube.com/watch ?v = zR3wbEudD 11.
Şi existenţa unei drepte care trece prin două puncte era presupusă de Euclid în primul postulat. În acest caz, problema construcţiei e, din multe puncte de vedere, mai complicată.
Mulţi sugerează să folosim o riglă, adică o bucată de material tăiat în lungul unei linii drepte: dar cum se construieşte o riglă?
Ajungem să ne întrebăm dacă se poate construi un compas pentru drepte, adică un mecanism articulat făcut din bare rigide prinse între ele la extremităţi şi ţinute eventual în acelaşi plan în care o extremitate se mişcă liber de-a lungul unei linii drepte.
O primă încercare în această direcţie a fost făcută chiar de James Watt (17 36-1819), inventatorul maşinii cu aburi. În CURBE
51


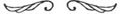
Figura 2.9
brevet, el a inserat şi descrierea unui mecanism articulat cu trei bare, cunoscut azi drept paralelogramul lui Watt, în care punctul mobil central e constrâns să se mişte aproape în linie dreaptă. Imaginea din stânga figurii 2.9 ilustrează mecanismul lui Watt. În dreapta, e desenată o aplicaţie care, la suspensiile automobilelor, exclude mişcările laterale nedorite în timpul oscilaţiilor verticale ale osiei vehiculului.
Iată descrierea lui Watt însuşi:
Am întrevăzut modul în care pot face un piston să se mişte în sus şi în jos perpendicular fixându-l doar de o bucată de fier pe ax, fără lanţuri sau şanţuri perpendiculare 1 .•• J, e unul dintre cele mai geniale şi simple instrumente mecanice pe care le-am inventat.
Dar mecanismul nu generează o mişcare rectilinie veritabilă
şi, de fapt, nici Watt nu a susţinut vreodată că ar face asta; el generează o curbă specială, numită „lemniscata lui Watt".
Primul mecanism adevărat care desenează o linie dreaptă a fost creat de un ofiţer francez, Charles-Nicolas Peaucellier (1832-1913). E vorba despre un paralelogram articulat cu şapte bare (vezi figura 2.10). Barele patrulaterului AQBP sunt toate egale între ele, la fel şi barele OA şi OB. Punctul O e fixat de plan, în timp ce punctul Pe constrâns să se mişte pe o circumferinţă care trece prin O (prins de o bară fixată la cealaltă extremitate 01.
Construcţia se bazează pe o transformare a planului care inversează punctele faţă de un cerc şi transformă în drepte cercurile care trec prin centrul cercului de inversiune.
52
FORMA LUCRURILOR


Descartes îşi pune pro
A.;..----; Q
blema generală de a găsi un
compas mecanic, format din
mai multe bare articulate între ele, pentru a desena orice curbă plană. Problema a fost
rezolvată pozitiv în 1875 de
B.A. Kempe, în articolul On a
General Method of Describing O;
Plane Curves of the n-th Degree
Figura 2.10
by Linkwork*. EI demonstrează
-şi încă destul de simplu-că orice curbă algebrică plană poate fi desenată cu un mecanism articulat (linkwork în engleză); definiţia curbei algebrice îi aparţine lui Descartes şi va fi discutată puţin mai departe.
Rezultatul acesta are numeroase aplicaţii care azi sunt teme de cercetare centrale în ingineria mecanică. Să luăm, de exemplu, următoarea problemă: date nouă puncte în plan, se poate demonstra că există un mecanism cu patru bare care desenează
o curbă care trece prin toate cele nouă puncte; dacă sunt mai mult de nouă puncte, e posibil ca problema să nu aibă soluţie.









