O asemenea ecuaţie e numită diferenţială pentru că leagă"'
între ele variabilele x şi y şi creşterile lor txx şi .1.y; ca s-o „rezolvăm", trebuie să scăpăm cumva de creşterile txx şi .1.y şi să obţinem, după
cum spunea Descartes, o ecuaţie care să lege numai x şi y.
Pentru asemenea probleme şi pentru altele asemănătoare au creat Johann Bemoulli, Leibniz şi Newton calculul diferen
ţial, dând astfel naştere unei puternice revoluţii conceptuale care va influenţa dezvoltarea succesivă a matematicii. Să încercăm să ne facem o idee despre această metodă nouă printr-un exemplu.
Să luăm benzile orizontale din figura 2.20 în care e împăr
ţit planul curbei; dacă ele sunt din ce în ce mai în guste, txx şi
.1.y devin elemente infinitezimale. Să presupunem că ecuaţia curbei e dată ca un grafic, adică îl putem exprima pe x în func
ţie dey, x =x(y).
Dacă rescriem ecuaţia dinainte sub forma
& = ✓ y l1y
c - y
putem spune că txx e egală cu aria unui dreptunghi cu baza .1.y şi cu înălţimea
✓c�y
Altfel spus, cele două dreptunghiuri gri din figura 2.21 au aceeaşi arie.
Privim acum zona notată pe figură A I ca fiind suma multor dreptunghiuri între O şi x; fiecărui dreptunghi dintre acestea îi corespunde în zona A 2 un dreptunghi de aceeaşi arie. Aşadar, presupunând că txx şi .1.y sunt suficient de mici (infinitezimale), ariile A I şi A 2 sunt egale.
De altfel, Bemoulli spune explicit: ergo fr horum integralia aequantur*; e prima apariţie, în matematică, a cuvântului integrală.
* Prin urmare aceste arii (integrale) sunt egale. (N. tr.) 74
FORMA LUCRURILOR


Al
/j. X
Figura 2.21
Am demonstrat deci că x(y), adică aria zonei A I, e egală cu aria de sub graficul funcţiei
dintre O şi y, adicăx(y) e integrala.funcţiei
✓c�y
Putem enunţa problema noastră şi folosind un alt concept fundamental din teoria calculului diferenţial, cel de derivată.
Dacă funcţia x(y) depinde suficient de continuu de y, făcându-l pe Liy arbitrar de mic, îl facem şi pe Lix arbitrar de mic. În plus, în anumite condiţii, raportul Lix/Liy tinde la o valoare precisă
pe care o numim derivata funcţiei x(y) în raport cu variabila y şi pe care o notăm
i(y) = lim tu
ăy➔ O �Y
CURBE
75
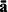
Cu această terminologie, ecuaţia brahistocronei se scrie ...
x(y) = ✓ Y
c - y
care e o ecuaţie diferenţială (cu variabile separate).
Aşadar, funcţia x(y) ejuncţia a cărei derivată este









