Cicloida îl interesează şi pe Christiaan Huygens (1629-1695), savant olandez genial care studiază sub îndrumarea lui Descartes şi anticipează multe rezultate din calculul diferen
ţial. Dar metoda lui e complet diferită de a lui Bernoulli. În cartea Horologium oscillatorium sive De motu pendulorum ad horologia aptato demonstrationes geometricae* (1673), Huygens îşi pune problema găsirii traiectoriei de-a lungul căreia un pendul se mişcă cu o perioadă independentă de amplitudinea iniţială. Căuta deci o curbă tautocronăpentru pendulul său, de la cuvintele greceşti -rau-ros (acelaşi) şi XQOVOS (timp).
Şi în acest caz ajungem la ecuaţie traducând în limbaj matematic trei observaţii.
Prima dintre ele se bazează pe principiul conservării cantităţii de mişcare descris de Newton; se presupune deci legea a doua a dinamicii, conform căreia forţa F care acţionează
asupra unui corp e egală cu produsul dintre masa m a corpului şi acceleraţie: F= ma. Prin definiţie, acceleraţia e derivata a doua a ecuaţiei de mişcare; deci, dacă s e lungimea arcului parcurs pe traiectorie, acceleraţia e dată de s, astfel că F= ms.
Proprietatea tautocronei se obţine cerând ca acceleraţia să
fie proporţională în fiecare punct cu lungimea arcului: s+Ks = O.
Se vede uşor că cele două triunghiuri din figura 2.23 sunt asemenea, deci laturile corespunzătoare sunt proporţionale: de aici obţinem F= -!:J.y/!1s.
Combinând cele trei formule obţinute prin observaţie, ob
ţinem ecuaţia
�y = Ks
* Ceasornicul cu pendul sau Demonstraţii geometrice privind mi?carea pendulului aplicată la ceasornice. (N. tr.)
78
FORMA LUCRURILOR

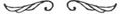

Integrând în raport cu varia-
bila s, găsim
K
y = -s2
2
adică
s = ft
Inserând această valoare a lui s
în egalitatea
�y = Ks
&
avem
Figura 2.23
�y = m & = m ✓Lix2 + �y2
✓Y
şi deci, după un mic calcul algebric, scriem ecuaţia diferen
ţială a brahistocronei sub forma
✓c�y �y = Lix
Până la o translaţie a variabileiy, e exact ecuaţia brahistocronei, deci şi în acest caz soluţia e o cicloidă- lucru observat chiar de Johann Bemoulli: animo revolvens inexpectatam illam identitatem tautochronae Hugeniae nostra que brachystocronae. Aşadar curba cicloidă e, în acelaşi timp, brahistocronă şi tautocronă.
Cicloida mai are o proprietate foarte utilă. Plecând de la o curbă plană fără puncte singulare, se poate construi o nouă curbă, numită evolventa (sau involuta) celei
de plecare, în modul următor: înfă
şurăm curba cu un fir inextensibil,
apoi desfăşurăm firul de pe curbă;









