Sunt foarte multe curbele care pot sta pe o suprafaţă; de exemplu, intersectând suprafaţa cu plane se obţin aşa-numitele sec
ţiuni plane.
Să fixăm două puncte pe o suprafaţă şi să considerăm toate curbele de pe ea care le unesc. O problemă naturală e găsirea, dacă există, a celei sau a celor de lungime minimă: o asemenea curbă se numeşte geodezică. Ne lovim adesea de această problemă în viaţa de zi cu zi: de exemplu, când mutăm obiecte pe un plan, ca să minimizăm efortul le deplasăm în linie dreaptă.
Sau la munte, în timpul unei drumeţii, când avem de traversat o vale, căutăm parcursul cel mai scurt ştiind prea bine că nu putem zbura, ci suntem obligaţi să rămânem pe suprafaţa terestră; alegerea unui traseu geodezic bun depinde de experienţă. De asemenea, când legăm un sul de hârtie cu o sfoară, aceasta se aşază de-a lungul unei geodezice a cilindrului format de sul.
SUPRAFEŢE 111

În general, un mod concret pentru a construi o geodezica e tocmai dispunerea unui fir bine întins între cele două puncte.
Căutarea unei geodezice între două puncte e o problemă
,,variaţională"; nu e deci de mirare că primul care şi-a pus problema in superficie quacumque ducere lineam inter duo puncta brevissima (trasarea liniei celei mai scurte între două puncte oarecare) a fost Johann Bemoulli, în 1697 . De fapt, ce voia el era să înţeleagă cum natura operari per modus et vias faciliores et expeditiores (operează natura prin mijloace şi căi mai uşoare şi mai rapide).
Bemoulli a studiat întâi problema pe suprafeţe de rotaţie, abia apoi pe suprafeţe generale; a introdus şi el conceptul de ecuaţie a unei suprafeţe, ca instrument necesar pentru obţinerea ecuaţiei geodezicei.
Geodezicele unei suprafeţe sunt caracterizate de o proprietate fundamentală care, dacă e formalizată matematic în mod convenabil, permite determinarea lor cu ajutorul ecuaţiilor.
Proprietatea derivă dintr-un procedeu folosit în topografie: se fixează doi ţăruşi pe suprafaţă, unul în punctul de plecare, A, şi unul într-un punct apropiat, B, în direcţia punctului în care trebuie să ajungem. Apoi se fixează ţăruşi în puncte succesive, C, D, ... , mereu în direcţia punctului în care vrem să ajungem, dar în aşa fel încât pentru un observator din A, ţăruşul din C să
fie ascuns de cel din B, pentru un observator din B, ţăruşul din D să fie ascuns de cel din C şi aşa mai departe, până ajungem în punctul fixat.
Procedând astfel în plan, obţinem o dreaptă - într-adevăr, geodezicele planului sunt dreptele.
Să încercăm acum să înţelegem această proprietate din punct de vedere matematic. Să observăm în primul rând că
ţăruşii sunt normali, adică perpendiculari pe suprafaţa S şi că, ţinând cont de felul cum îi dispunem, fiecare stă într-un plan care trece prin punctul precedent şi prin cel succesiv. Trecând la limită, adică presupunând că punctele A, B, C etc. se apropie indefinit unul de altul, planul acesta va coincide cu planul osculator al curbei căutate; aşadar, planul osculator în orice punct 112 FORMA LUCRURILOR

al unei geodezice conţine dreapta normală la suprafaţă în acel punct, adică planul osculator la geodezică e normal la suprafaţă.
De altfel, cu tehnica firului întins între două puncte pe suprafaţă, Johann Bemoulli a observat că, pentru a menţine firul în echilibru, planul osculator trebuie să fie normal la suprafaţă.
Avem deci două definiţii ale curbei geodezice, una mai intuitivă - curba cea mai scurtă între două puncte -, a doua mai formalizată - curba al cărei plan osculator în orice punct con
ţine dreapta normală la suprafaţă în acel punct. Să observăm că prima e o proprietate internă, sau intrinsecă, a suprafeţei, punctele din spaţiul ambient al suprafeţei neintervenind, în timp ce a doua e o proprietate exterioară care depinde, prin intermediul dreptei normale şi a planului osculator, de felul cum e poziţionată suprafaţa în spaţiul ambient.
Am observat deja că prima definiţie o implică pe a doua.
Faptul că o curbă pe suprafaţă având proprietatea că planul său osculator conţine dreapta normală la suprafaţă e o curbă
de lungime minimă e mai delicat de verificat şi e adevărat numai dacă acea curbă e cuprinsă într-o regiune mică a suprafeţei - spunem că e o proprietate locală.
Dacă suprafaţa e definită cu ecuaţii (carteziene sau parametrice) definiţia cu planul osculator conduce la ecuaţia diferenţială
a geodezicei; soluţia ei fumizează, cel puţin local, ecuaţia curbei geodezice. Tipul de calcule necesare e asemănător celor făcute pentru brahistocronă în capitolul precedent, iar dificultatea lor depinde şi de complexitatea ecuaţiei suprafeţei.
Metoda ţăruşilor sugerează că din orice punct al suprafeţei izvorăsc o infinitate de geodezice, anume câte una în fiecare direcţie tangentă la suprafaţă. Direcţia geodezicei din punctul P se numeşte condiţie iniţială; se poate arăta că soluţia ecuaţiei diferenţiale a geodezicelor depinde univoc de această condiţie iniţială: fixată direcţia, există (local) o singură soluţie.
Când căutăm geodezicele pe suprafaţa terestră cu metoda topografică, nu vom ajunge să trasăm linii drepte (de altfel, nici nu există drepte pe sferă). Vom obţine de fapt porţiuni de SUPRAFEŢE
113

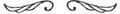

cercuri maxime, obţinute priiî
intersectarea sferei cu un plan
care trece prin cele două
puncte şi prin origine, ca în figura 3.22.
Figura 3.22
Pe de altă parte, e evident
că cercurile maxime sunt singurele curbe pe sferă ale căror plane osculatoare conţin normalele la sferă în fiecare punct.
În manieră empirică, aşa cum proceda Bemoulli (rationem experientiae), putem şi să întindem bine o coardă între două









