ţia cosinus se anulează, deciy(t) ar lua o valoare infinită.
Există şi alte corespondenţe conforme între sferă şi plan. De exemplu, proiecţia stereografică (faţă de Polul Nord) care asociază
fiecărui punct P de pe sferă, diferit de Polul Nord, punctul din planul tangent în Polul Sud obţinut ca intersecţie dintre acest plan şi dreapta care trece prin Popul Nord şi prin P, ca în figura 3.34.
Polul Nord
Figura 3.34
SU PRAFEŢE 129
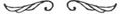


Figura 3.35
Se pot însă construi şi corespondenţe între sferă şi plan care să păstreze alte proprietăţi geometrice, de exemplu proiecţii care păstrează ariile, numite proiecţii echivalente. Matematicianul şi cartograful Johann Heinrich Lambert a construit una în 17 7 2; în 197 3, istoricul Amo Peters a propus o alta, care anulează multe convenţii geografice şi, în consecinţă, chiar istorice.
A fost numită proiecţia Call-Peters pentru că se pare că a fost folosită pentru prima dată în 1885, de James Gall, preot scoţian.
În figura 3.35 apar o proiecţie stereografică şi una Gall-Peters.
GEOMETRI N EEUCLIDIENE
Să examinăm din nou formula lui Gauss pentru aria triunghiului (geodezic) sferic, Ar=R 2 • (a +p+ y - n)
Conform acestei formule, în orice triunghi sferic, suma unghiurilor interne e mai mare decât n, iar excesul e proporţional cu aria triunghiului.
Am învăţat însă la şcoală că, aşa cum e demonstrat în Elemente, suma unghiurilor interne ale unui triunghi e egală cu 180 de grade. Nu e nici o încurcătură: la şcoală lucrăm numai cu triunghiuri plane, nu cu triunghiuri sferice.
130 FORMA LUCRURILOR

Formula lui Gauss sugerează că o teorie geometrică, măsurile şi teoremele ei depind de spaţiul care găzduieşte obiectele ei de studiu.
Una dintre marile noutăţi ale concepţiei lui Gauss constă
tocmai în considerarea suprafeţelor ca spaţii autonome, adică
non tamquam limes solidi, sed tamquam solidum cuius dimensio unapro evanescente habetur(nu ca frontiere de corpuri solide, ci ca niW
corpuri solide la care una dintre dimensiuni dispare). Ca să înţelegem mai bine noutatea conţinută în această afirmaţie, vă propun să înlocuim cuvântul solid cu spaţiu, deci să spunem că suprafaţa e „un spaţiu cu o dimensiune care dispare".
Reverendul Edwin Abbott a introdus acest punct de vedere şi în domeniile artistic şi social, într-un scurt roman satiric despre societatea victoriană, intitulat Flatland (1884), a cărui acţiune se desfăşoară într-o ipotetică lume bidimensională.
Locuitorii acestei lumi sunt figuri geometrice care trăiesc într-un spaţiu bidimensional în care reuşesc totuşi să reproducă
unele caracteristici şi contradicţii ale societăţii timpului. Cel puţin din punct de vedere artistico-narativ, romanul demonstrează că un spaţiu cu două dimensiuni poate găzdui o societate, poveşti şi fiinţe dotate cu raţiune. Existenţa unei a treia dimensiuni, evanescentă în spaţiul din Flatland, apare abia în partea a doua, când asistăm la întâlnirea dintre un pătrat cu o sferă, un obiect care provine dintr-un spaţiu tridimensional numit Spaceland.*
Aşadar, o suprafaţă poate fi concepută foarte bine drept spaţiu autonom, bidimensional, în care se poate construi o geometrie.
Nimic nou, s-ar zice, faţă de ce a făcut Euclid, care şi-a dezvoltat întreaga geometrie pe plan. Dar sunt atât de multe suprafeţe, nu doar planul. Ideea că spaţiul ambient nu e unic e cu adevărat contraintuitivă; să ne aducem aminte cuvintele lui Kant, citate în primul capitol.
* Există şi un foarte frumos film de animaţie (pe computer) după
cartea lui Edwin Abbott, în acces liber aici: https://www.youtube.com/
watch?v = eyuNrm4VK2w. (N. tr.)
SUPRAFEŢE 131

Dacă dezvoltăm o geometrie cu aceleaşi axiome şi reguli, dar în spaţii ambiente-suprafeţe diferite ne aşteptăm la teorii diferite, după cum se vede în teorema egregium.
Curbele geodezice se pot defini pe orice suprafaţă ca fiind cele mai scurte. Dacă suprafaţa e completă, aceste curbe geodezice satisfac cele patru cerinţe ale lui Euclid pentru dreapta din plan, aşa cum am văzut la sfârşitul paragrafului despre geodezice. Şi triunghiul geodezic (la fel şi celelalte poligoane) are o definiţie generală: constă în trei segmente geodezice cu proprietatea că oricare două dintre ele au un singur vârf în comun.
Triunghiurile geodezice au totuşi proprietăţi diferite după
cum sunt sferice sau plane: de exemplu, aşa cum am demonstrat, suma unghiurilor lor interne e diferită.
Se poate arăta că enunţul: ,,suma unghiurilor interne ale unui triunghi e 180 de grade" e echivalent cu Postulatul V al lui Euclid. Dar acest postulat nu subzistă în geometria sferică: dată o dreaptă pe sferă (un cerc maxim), prin nici un punct exterior nu există vreo dreaptă paralelă la dreapta de plecare.
Într-adevăr, pe sferă nu există drepte paralele, pentru că orice două cercuri maxime se întâlnesc (în exact două puncte)!









