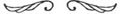
...
X
y
• --
- !□
w
. �
·,, '
'
�
o
1
2
3
4
#Dim
Figura 4.1
gândită ca o sinteză dintre o variabilitate n-dimensională şi o variabilitate I-dimensională.
Figura 4.1 ilustrează construcţia unui „cub" în orice dimensiune; se pleacă de la un punct (dimensiune O) care e translatat în linie dreaptă într-o anumită direcţie, obţinând astfel un segment (dimensiune I). Se continuă, translatând în linie dreaptă
figura într-o direcţie ortogonală pe cea dintâi, obţinând un pătrat; apoi, translatând într-o direcţie perpendiculară pe primele două, se obţine un cub în spaţiu (deja, desenul reprezintă o proiecţie plană a cubului), apoi un „hipercub" 4-dimensional şi aşa mai departe, se obţin „cuburi" în orice dimensiune.
Riemann propune câteva exemple de varietăţi: primul e destul de naiv şi e dat de mulţimea formată de culori. Mulţimea depinde de trei parametri, cele trei culori fundamentale (albastru, roşu şi verde); orice altă culoare e dată de o combinaţie anume a celor trei culori fundamentale.
Exemplul principal e dat de suprafeţele descrise de Gauss, varietăţi de dimensiune 2. În capitolul al treilea, observasem că
o suprafaţă poate fi descrisă sub formă parametrică, drept mul
ţime a punctelor spaţiului ale căror coordonate carteziene (x(u, v),y(u, v),z(u, v)) sunt date de funcţii x(u, v), y(u, v) şi z(u, v) care depind de doi parametri continui u şi v. Sfera de rază r centrată în origine, de exemplu, e descrisă cu parametrii latitudine şi longitudine de funcţiile (x(u, v),y(u, v),z(u, v))= (rsinvcosu,rsinv sinu,rcosv). Am văzut şi că există mai multe tipuri de hărţi geografice, deci mai multe moduri de a parametriza şi de a da coordonate.
148 FORMA LUCRURILOR
Variind parametrii u şi v, parcurgem întreaga suprafaţă fără
să mai ţinem seama de spaţiul obişnuit în care e scufundată
suprafaţa.
În lucrări ulterioare, Riemann va relua conceptul de varietate pentru a studia probleme noi şi complexe. Va propune chiar şi un exemplu foarte particular, anume varietatea formată
de toate suprafeţele: o mulţime de mulţimi! Aceasta se numeşte spaţiu de moduli şi e probabil cea mai studiată în geometria contemporană. Riemann o descrie cu instrumente inovative, printre care teoria funcţiilor regulate care depind de o variabilă
complexă (funcţii olomorfe) şi-i determină dimensiunea.
Observă, de asemenea, că există varietăţi care nu pot fi determinate folosind un număr finit de variabile independente; sunt deci varietăţi în care o poziţie e specificată de o infinitate de parametri. Ca exemplu de asemenea varietate infinit dimensională dă mulţimea funcţiilor dintr-o regiune, ori formele unei figuri solide.
Cu această observaţie, Riemann demonstrează încă o dată
o profundă înţelegere a obiectelor matematice; varietăţile de dimensiune infinită sunt extrem de utile în analiză, iar studiul lor prezintă un nivel de complexitate foarte înalt.
Pentru Riemann, o varietate nu e doar mărime multiplu extinsă, ci e pasibilă de diverse relaţii metrice. AI doilea capitol al disertaţiei lui Riemann are tocmai titlul „Metrici [Massverhaltnisse] posibile într-o varietate n-dimensională în ipoteza că curbele au o lungime independentă de poziţie ... "*
Pe o varietate, vrem să măsurăm distanţa dintre două entităţi, vrem să calculăm mărimea unei submulţimi care, în func
ţie de dimensiune, poate fi o lungime, o arie, un volum sau un hipervolum. În acest scop, Riemann introduce conceptul de metrică pe varietate, apoi pe acela de curbură, luând în mod explicit ca exemplu construcţiile lui Gauss pentru suprafeţe.









